伽罗华域傅里叶变换(GFFT)是识别RS码编码参数的一种非常有效的方法。与传统的欧几里得分析法[1-2]和矩阵分析法[3-6]相比,GFFT分析法在抗误码方面具有明显的优势,已成为目前RS码的主流分析方法[7-13],并且已形成完善的理论体系[10-11]。但是,现有文献中所涉及的研究对象都是非缩短的RS码,而缩短RS的应用更为广泛,因此非常有必要讨论缩短RS的识别问题。本文把有限长度GFFT拓展到任意长度,使其能够适用于缩短RS码,并利用文献[10]中的类似方法,定义缩短RS码谱累积量,根据其概率分布确定判决门限,从而得到缩短RS码的GFFT识别方法,解决了缩短RS码的识别问题。
1 缩短RS码的谱累积量 1.1 任意长度GFFT经典GFFT(限定长度GFFT)要求序列长度必须为
令
| $ V(x) = {V_0} + {V_1}x + \cdots + {V_{n - 1}}{x^{n - 1}} $ | (1) |
式中
| $ {V_j} = v({\alpha ^j}) = \sum\limits_{i = 0}^{l - 1} {{v_i}{\alpha ^{ij}}} ,\;\;\;j = 0,1, \cdots ,n - 1 $ | (2) |
为
由任意长GFFT的定义可知:a)多项式
假设
| $ g(x) = (x - \alpha )(x - {\alpha ^2}) \cdots (x - {\alpha ^{2t}}) $ | (3) |
式中
如果从
令
参考文献[10]定义
| $ {V_k} = ({V_{k, 0}}, {V_{k, 1}}, \cdots , {V_{k, n - 1}}) $ | (4) |
则可得到
| $ W = ({W_0}, {W_1}, \cdots , {W_{n - 1}}) $ | (5) |
式中
| $ {W_j} = \sum\limits_{k = 1}^M {{V_{k, j}}} , \;j = 0, 1, \cdots , n - 1 $ | (6) |
根据
1) 码长为真实码长,并且GFFT参数与RS码编码参数相同。假设接收误码率为
| $ \left\{ \begin{array}{l} {E_1} = E\{ {W_r}\} = \frac{{Mn}}{2}\left[ {1 - {{(1 - \varepsilon )}^{{n_1}}}} \right] \\ {D_1} = D\{ {W_r}\} = \frac{{Mn(2n + 1)}}{6}\left[ {1 - {{(1 - \varepsilon )}^{{n_1}}}} \right] - \frac{{M{n^2}}}{4}{\left[ {1 - {{(1 - \varepsilon )}^{{n_1}}}} \right]^2} \\ \end{array} \right. $ | (7) |
| $ \left\{ \begin{array}{l} {E_0} = E\{ {W_{nr}}\} = \frac{{Mn}}{2} \\ {D_0} = D\{ {W_{nr}}\} = \frac{{Mn(n + 2)}}{{12}} \\ \end{array} \right. $ | (8) |
另外,在接收端通常给出的误比特率而不是误码率,需要进行转换。假设接收误比特率为
| $ \varepsilon = 1 - {\left( {1 - \tau } \right)^m} $ | (9) |
重写
| $ \left\{ \begin{array}{l} {E_1} = \frac{{Mn}}{2}\left[ {1 - {{(1 - \tau )}^{m{n_1}}}} \right] \\ {D_1} = \frac{{Mn(2n + 1)}}{6}\left[ {1 - {{(1 - \tau )}^{m{n_1}}}} \right] - \frac{{M{n^2}}}{4}{\left[ {1 - {{(1 - \tau )}^{m{n_1}}}} \right]^2} \\ \end{array} \right. $ | (10) |
2) 其他情况。若码字为随机码字,则其根在有限域上也是随机分布的,即此时累积量中每个分量的分布都与情况1)中谱分量
由上述可知,缩短RS码谱累积量的分量近似服从2个不同均值和方差的高斯分布,其概率密度分布分别为:
| $ {p_0}(x) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}{D_0}} }}\exp \left[ {\frac{{ - {{(x - {E_0})}^2}}}{{2{D_0}}}} \right] $ | (11) |
| $ {p_1}(x) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}{D_1}} }}\exp \left[ {\frac{{ - {{(x - {E_1})}^2}}}{{2{D_1}}}} \right] $ | (12) |
式中:
缩短RS码的识别包括域的识别、码长的识别以及生成多项式的识别,域的识别又包括阶数
由1.3中讨论可知,当阶数、本原多项式、码长都与实际参数相同时,谱累积量中存在分量服从概率分布
| $ H = \left\{ \begin{gathered} {H_1}\begin{array}{*{20}{c}} {}&{\exists j, }&{1 \leqslant j \leqslant n, }&{{W_j} \leqslant T} \end{array} \\ {H_0}\begin{array}{*{20}{c}} {}&{\forall j, }&{1 \leqslant j \leqslant n, }&{{W_j} > T} \end{array} \\ \end{gathered} \right. $ | (13) |
式中:
在成功完成阶数、本原多项式及码长的识别后,统计谱累积量中小于等于阈值的连续分量的个数
| $ \hat g(x) = (x - \alpha )(x - {\alpha ^2}) \cdots (x - {\alpha ^{2\hat t}}) $ | (14) |
在2.1识别方法中,阈值的选取是影响识别性能的关键。由于已经获取
如果选定的阈值为T,则虚警概率和漏警概率分别为:
| $ {P_{\rm{f}}} = \int_{ - \infty }^T {{p_0}(t){\rm{d}}t} = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}{D_0}} }}\int_{ - \infty }^T {\exp \left[ {\frac{{ - {{(t - {E_0})}^2}}}{{2{D_0}}}} \right]{\rm{d}}t} $ | (15) |
| $ {P_{\rm{n}}} = \int_T^\infty {{p_1}(t){\rm{d}}t} = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}{D_1}} }}\int_T^\infty {\exp \left[ {\frac{{ - {{(t - {E_1})}^2}}}{{2{D_1}}}} \right]{\rm{d}}t} $ | (16) |
以
| $ T = \frac{{{E_0}\sqrt {{D_1}} + {E_1}\sqrt {{D_0}} }}{{\sqrt {{D_0}} + \sqrt {{D_1}} }} $ | (17) |
可见,
令
| $\alpha = \frac{{{E_0} - {E_1}}}{{\sqrt {{D_0}} + \sqrt {{D_1}} }} = \frac{{{E_0} - T}}{{\sqrt {{D_0}} }} = \frac{{T - {E_1}}}{{\sqrt {{D_1}} }} $ | (18) |
此时,
| $ {P_{\rm{f}}} = {P_{\rm{n}}} = \int_\alpha ^\infty {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} }}\exp \left( {\frac{{ - {t^2}}}{2}} \right){\rm{d}}t} = Q(\alpha ) $ | (19) |
显然
| $ \frac{{{E_0} - {E_1}}}{{\sqrt {{D_0}} + \sqrt {{D_1}} }} \geqslant 3 $ | (20) |
代入
| $ M \geqslant 9{\left( {\frac{{\sqrt {{d_1}} + \sqrt {{d_0}} }}{{{e_0} - {e_1}}}} \right)^2} $ | (21) |
式中:
如果取定
| $ \tau \leqslant 1 - {\left( {\frac{{2\sqrt {3Mn(n + 2)} + 6(n - 1)}}{{9n + Mn}}} \right)^{1/m{n_1}}} $ | (22) |
此外,当
综上所述:a)误码适应能力评估:码字数、编码参数确定条件下,根据式(22),估计所能适应的误比特率;b)数据量需求评估:误比特率、编码参数确定条件下,可根据式(21)估计所需要的数据量;c)算法有效性评估:如果
本试验验证2.3中数据量误码适应能力评估方法的正确性。以
| 表 1 α=3和M=50时(31, 29)RS码生成的缩短RS码不同码长对应的最大误比特率 Table 1 Maximal bit error rate of different code lengths for shortened RS code from (31, 29)RS when α=3 and M=50 |
根据表 1数据可以预期,当误比特率分别取0.004, 0.006, 0.008和0.010时,如果对应码长不大于31, 21, 16和12,则可获得较好识别性能。为此,误比特率分别取0.004, 0.006, 0.008和0.010,进行仿真试验,在每种码长下,试验1 000次,统计正确识别率。
图 1给出了误比特率为0.01时的仿真结果。从结果中可以看出:阶数的正确识别率明显优于其他参数;码长、本原多项式、生成多项式的正确识别率随码长增加而降低,这是由于当码字数和误比特率固定时,α随码长的增加而减小从而导致正确识别率降低。其他误码率条件下的仿真结果类似。阶数的识别性能之所以远优于其他参数,是由于不论本原多项式是否正确,只要满足判决条件,则可正确识别,显然不适合以阶数作为对比参数。这里以码长作为待识别参数进行对比。
 |
| Fig.1 Correct recognition rate of different parameters when τ=0.01 图 1 τ=0.01 时不同参数的正确识别率 |
图 2给出了不同误码率条件下码长的正确识别率曲线。从图 2(a)中可以看出,识别性能随误比特率增加而恶化。图 2(b)对图 2(a)进行了局部放大。由图 2(b)可知,当误比特率0.004,码长31时,正确识别率为0.976;以0.976为阈值,可以得到误比特率为0.006, 0.008和0.001时,正确识别率大于0.976所对应的码长分别为21, 16和13,与理论分析基本一致,所以验证了2.3中误码适应能力评估方法的正确性。
 |
| Fig.2 Correct recognition rate of code length for different bit error rates 图 2 不同误比特率条件下码长正确识别率 |
本次仿真试验验证2.3中数据量需求评估方法的正确性。仍以(31, 29)RS码生成的缩短RS码为例进行仿真分析,其他参数同3.1。给定误比特率为0.01,则根据式(21)可得到,α时对应的最小M值见表 2。
| 表 2 τ=0.01和α=3时(31, 29)RS码生成的缩短RS码不同码长对应的最小M值 Table 2 Minimal M of different code lengths for shortened RS code from (31, 29)RS when τ=0.01 and α=3 |
根据表 2可以预期,当码字数分别取50, 100, 200, 325时,如果对应码长不大于12, 19, 26, 31,则可获得较好识别性能。为此,码字数分别取50, 100, 200和325,进行仿真试验,在每种码长下,试验1 000次,统计正确识别率,仿真结果见图 3。从图 3(a)中可以看出,识别性能随码字数增加而提高。图 3(b)对图 3(a)进行了局部放大。由图 3(b)可知,当码字数取325时,码长31时的正确识别率为0.971;以0.971为阈值,可以得到码字数为50, 100, 200时,正确识别率大于0.971所对应的码长分别为13, 20和26,与理论分析基本一致,从而验证了2.3中数据量估计方法的正确性。
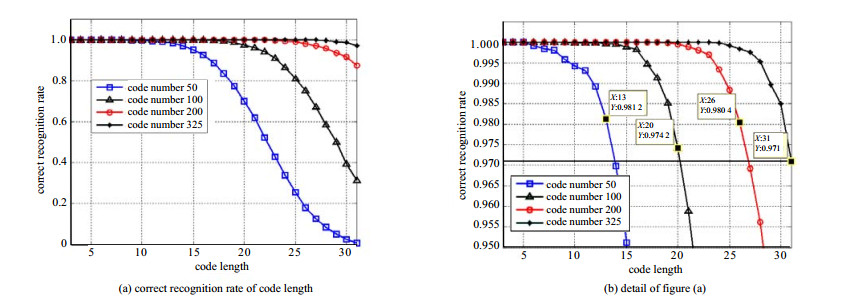 |
| Fig.3 Correct recognition rate of code length for different code numbers 图 3 不同码组数下码长正确识别率(τ=0.01) |
实际应用中,RS码的阶数一般不会超过8,可选定阶数为3~8。此外,实际的处理平台的处理能力及硬件资源总是有限,所以
首先根据
随机选取阶数、码长、最大纠错数、本原多项式进行仿真试验,
 |
| Fig.4 Simulation results for RS code with randomly selected parameters 图 4 随机选取缩短RS码参数时的仿真结果 |
值得说明的是,按照2.3中评估方法,当
本文把用于非缩短RS码GFFT识别方法经过拓展后应用于缩短RS码的识别,并给出了缩短RS码GFFT谱累积量的概率分布及阈值确定方法。在此基础上,从理论上分析了误码适应性、数据量需求以及算法有效性的评估方法,从而建立了完整的理论体系,为识别算法的实际应用提供了理论依据。仿真试验在验证算法性能的同时,也证明了理论分析的正确性。尽管如此,从理论分析和仿真可以看出,当RS码的阶数较大(例如阶数大于8)或误码率更高(例如误比特率为0.01)时,很难获得较好的识别性能,或者所付出的代价是难以承受的,因此如何提高算法在高阶、高误码条件下的性能是当前亟需解决的问题。
| [1] |
戚林, 郝士琦, 李今山. 基于有限域欧几里德算法的RS码识别[J]. 探测与控制学报, 2011, 33(2): 63-67. (QI Lin, HAO Shiqi, LI Jinshan. Recognition method of RS codes based on Euclidean algorithm in Galois field[J]. Journal of Detection & Control, 2011, 33(2): 63-67. DOI:10.3969/j.issn.1008-1194.2011.02.015) |
| [2] |
甘露, 周攀. 基于中国剩余定理分解的RS码快速盲识别算法[J]. 电子与信息学报, 2012, 34(12): 2837-2842. (GAN Lu, ZHOU Pan. Fast blind recognition method of RS codes based on Chinese remainder theorem decomposition[J]. Journal of Electronics & Information Technology, 2012, 34(12): 2837-2842.) |
| [3] |
杨晓静, 闻年成. 基于秩函数和Euclide算法的循环码盲识别[J]. 电路与系统学报, 2011, 17(5): 120-124. (YANG Xiaojing, WEN Niancheng. A blind method of cyclic codes based on rank function and Euclide arithmetic[J]. Journal of Circuits and Systems, 2011, 17(5): 120-124.) |
| [4] |
闻年成, 杨晓静, 白彧. 一种新的RS码识别方法[J]. 电子信息对抗技术, 2011, 26(2): 36-40. (WEN Niancheng, YANG Xiaojing, BAI Yu. A new recognition method of RS codes[J]. Electronic Information Warfare Technology, 2011, 26(2): 36-40. DOI:10.3969/j.issn.1674-2230.2011.02.008) |
| [5] |
LI Wenwen, LEI Jing, WEN Lei. An improved method of blind recognition of RS code based on matrix transformation[C]// 15th IEEE International Conference on Communication Technology Proceedings. Guilin, China: IEEE, 2013: 196-200.
|
| [6] |
朱联祥, 李荔. RS码的盲识别方法研究[J]. 电子测量与仪器学报, 2013, 27(8): 781-787. (ZHU Lianxiang, LI Li. Research on blind recognition for RS code[J]. Journal of Electronic Measurement and Instrument, 2013, 27(8): 781-787.) |
| [7] |
刘健, 谢锯, 周希元. RS码的盲识别方法[J]. 电子科技大学学报, 2009, 38(3): 363-367. (LIU Jian, XIE Ju, ZHOU Xiyuan. Blind recognition method of RS coding[J]. Journal of University of Electronic Science and Technology of China, 2009, 38(3): 363-367. DOI:10.3969/j.issn.1001-0548.2009.03.011) |
| [8] |
闻年成, 杨晓静. RS码的盲参数识别[J]. 计算机工程与应用, 2011, 47(19): 136-139. (WEN Niancheng, YANG Xiaojing. Blind recognition of RS codes parameters[J]. Computer Engineering and Applications, 2011, 47(19): 136-139. DOI:10.3778/j.issn.1002-8331.2011.19.037) |
| [9] |
王平, 曾伟涛, 陈健. 一种利用本原元的快速RS码盲识别算法[J]. 西安电子科技大学学报(自然科学版), 2013, 40(1): 105-110. (WANG Ping, ZENG Weitao, CHEN Jian. Fast blind recognition algorithm for RS codes by primitive element[J]. Journal of Xidian University, 2013, 40(1): 105-110. DOI:10.3969/j.issn.1001-2400.2013.01.019) |
| [10] |
XIE Hui, WANG Fenghua, HUANG Zhitao. Blind recognition of Reed-Solomon codes based on histogram statistic of Galois field spectra[J]. Advanced Materials Research, 2013(791-793): 2088-2091. |
| [11] |
王丰华, 解辉, 黄知涛, 等. 基于频谱累积量的线性分组码检测识别方法[J]. 系统工程与电子技术, 2013, 35(12): 2595-2599. (WANG Fenghua, XIE Hui, HUANG Zhitao, et al. Blind recognition of linear block code based on spectral cumulants[J]. Systems Engineering and Electronics, 2013, 35(12): 2595-2599. DOI:10.3969/j.issn.1001-506X.2013.12.25) |
| [12] |
解辉, 王丰华, 黄知涛, 等. 基于频谱预处理的RS码盲检测识别方法[J]. 宇航学报, 2013, 34(1): 128-132. (XIE Hui, WANG Fenghua, HUANG Zhitao, et al. Blind detection and recognition of RS code based on spectral preprocessing[J]. Journal of Astronautics, 2013, 34(1): 128-132. DOI:10.3873/j.issn.1000-1328.2013.01.018) |
| [13] |
包昕, 陆佩忠, 游凌. 基于伽罗华域傅里叶变换的RS码识别方法[J]. 电子科技大学学报, 2016, 45(1): 30-35. (BAO Xin, LU Peizhong, YOU Ling. Recognition of RS coding based on Galois Field Fourier Transform[J]. Journal of University of Electronic Science and Technology of China, 2016, 45(1): 30-35.) |
 2020, Vol. 18
2020, Vol. 18


